[Vector] 두 벡터 사이의 각도 구하기 (내적/외적)

내적으로 두 벡터의 사이각 구하기 (0 ~ 180도)

수학에서 두 벡터 사이의 각도 (사이각) 은 0 ~ 180도 사이의 값으로 정의된다.
두 벡터 $\vec{\alpha}$ , $\vec{\beta}$ 의 사이각을 $\theta$ 라 할 때, 사이각 $\theta$ ($0\leq\theta<\pi$) 는 내적과 역삼각함수로 구할 수 있다.

$$\vec{\alpha}\cdot\vec{\beta} = |\vec{\alpha}||\vec{\beta}|cos\theta$$

$$cos\theta = \frac{\vec{\alpha}\cdot\vec{\beta} }{|\vec{\alpha}||\vec{\beta}|}$$
$$\therefore\theta = cos^{-1}(\frac{\vec{\alpha}\cdot\vec{\beta} }{|\vec{\alpha}||\vec{\beta}|}) = acos(\frac{\vec{\alpha}\cdot\vec{\beta}}{|\vec{\alpha}||\vec{\beta}|})$$
$$(단, 0\leq\theta<\pi)$$

내적으로 구한 사이각이 항상 0 ~ 180도 사이 값인 이유는 $cos\theta$ 값이 $\pi$ 를 기점으로 대칭이 되기 때문이다.
역함수인 $\theta = acos(y) $를 사용하기 위해서는 하나의 $y$ 값에 하나의 $\theta$ 값만 필요하므로, $\theta$의 범위를 $0\leq\theta<\pi$ 으로 제한한다.

$0\leq\theta\leq2\pi$ 일 때, $cos\theta = 0$ 인 $\theta$ 는 2가지 값($\frac{\pi}{2}, \frac{3\pi}{2}$)이 될 수 있다.

 

내/외적으로 두 벡터의 사이각 구하기 (0 ~ 360도)

180도가 넘는 사이각이 필요할 때가 있다.
두 벡터 $\vec{\alpha}$ , $\vec{\beta}$ 와 수직인 벡터 $\hat{n}$ 을 알고 있다면, 외적으로 두 벡터의 사이각의 크기가 180도 미만인지 이상인지 알 수 있다.

$\hat{n}$ 을 회전축 삼아 첫번째 벡터를 반시계방향으로 두번째 벡터까지 회전시켰을 때,
회전각이 180도 이상이면 외적의 결과 벡터 $\vec{\alpha}\times\vec{\beta}$ 는 $\hat{n}$ 과 반대 방향이 된다.

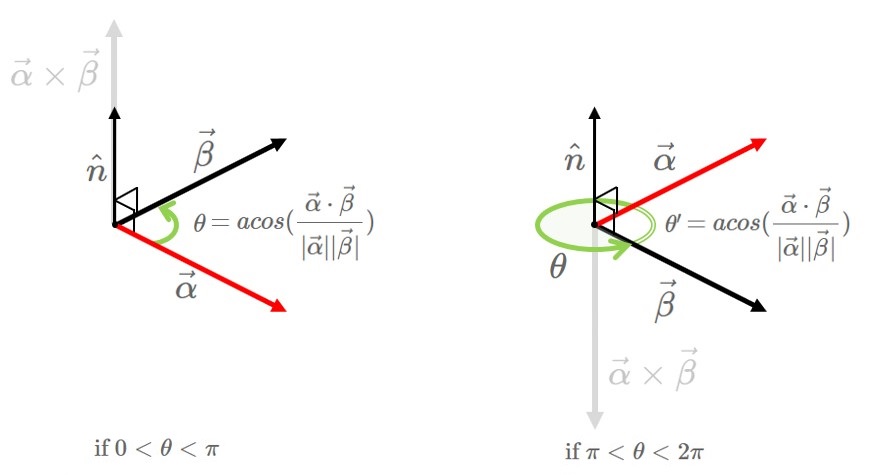
$\vec{\alpha}\times\vec{\beta}$ 와 $\hat{n}$ 이 같은 방향인지 판별하는 방법은 여러가지가 있다.

가장 간단한 방법은 $\vec{\alpha}\times\vec{\beta}$ 의 요소 (x, y, z) 중 하나를 구해서 $\hat{n}$ 의 요소와 부호를 비교하는 것이다.

 

$$\text{Let }\vec{\alpha}\text{ =  }(a.x, a.y, a.z)\text{ and }\vec{\beta}\text{ = }(b.x, b.y, b.z)$$

$$(\vec{\alpha}\times\vec{\beta}).z\text{ = a.x * b.y - a.y * b.x}$$

$$\hat{n}\text{ and }\vec{\alpha}\times\vec{\beta}\text{ are in same direction if }(\vec{\alpha}\times\vec{\beta}).z * \hat{n}.z > 0$$

 

즉 두 벡터의 내적으로 구한 사이각을 $\theta'$ ($0\leq\theta'<\pi$) 라고 할 때, 실제 사이각 $\theta$ ($0\leq\theta<2\pi$) 는 다음과 같다.

$$\vec{\alpha}\times\vec{\beta} = \hat{n} |\vec{\alpha}||\vec{\beta}|sin\theta$$

$$( \hat{n} \text{ is a vector that }|\hat{n}| = 1, \vec{\alpha} \perp \hat{n}, \vec{\beta} \perp \hat{n})$$
$$\therefore\theta=\begin{cases}\theta' & \quad \text{if } (\vec{\alpha}\times\vec{\beta}).z * \hat{n}.z \geq 0\\2\pi-\theta' & \quad \text{if } (\vec{\alpha}\times\vec{\beta}).z * \hat{n}.z<0\end{cases}$$

$|\vec{\alpha}\times\vec{\beta}|=0$ 일 때는 $cos\theta'$ 값이 1 또는 -1 임을 이용해 판별할 수 있다.